This notebook contains edits from Udacity
¶ Introduction to Neural Networks with TensorFlow
In this notebook, you'll get introduced to TensorFlow, an open source library to help you develop and train machine learning models.
TensorFlow in a lot of ways behaves like the arrays you love from NumPy. NumPy arrays, after all, are just tensors. TensorFlow takes these tensors and makes it simple to move them to GPUs for the faster processing needed when training neural networks. TensorFlow can also calculate gradients automatically, which is perfect for backpropagation, and has intuitive high-level APIs specifically for building neural networks.
¶ Neural Networks
Deep Learning is based on artificial neural networks which have been around in some form since the late 1950s. The networks are built from individual parts approximating neurons, typically called units or simply "neurons." Each unit has some number of weighted inputs. These weighted inputs are summed together (a linear combination) then passed through an activation function to get the unit's output.

Mathematically, the above looks like:
where,
If we let , then we can express as the dot/inner product of two vectors:
¶ Tensors
It turns out neural network computations are just a bunch of linear algebra operations on tensors, a generalization of matrices. A vector is a 1-dimensional tensor, a matrix is a 2-dimensional tensor, an array with three indices is a 3-dimensional tensor (RGB color images for example). The fundamental data structure for neural networks are tensors and TensorFlow is built around tensors.
With the basics covered, it's time to explore how we can use TensorFlow to build a simple neural network.
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import tensorflow as tf
# Set the random seed so things are reproducible
tf.random.set_seed(7)
# Create 5 random input features
features = tf.random.normal((1, 5))
# Create random weights for our neural network
weights = tf.random.normal((1, 5))
# Create a random bias term for our neural network
bias = tf.random.normal((1, 1))
print('Features:\n', features)
print('\nWeights:\n', weights)
print('\nBias:\n', bias)
Features:
tf.Tensor([[ 0.5983449 0.06276207 0.14631742 0.4848188 -0.23572342]], shape=(1, 5), dtype=float32)
Weights:
tf.Tensor([[-2.2733312 -1.6592104 -0.2633568 -0.8092342 1.0294315]], shape=(1, 5), dtype=float32)
Bias:
tf.Tensor([[1.5749502]], shape=(1, 1), dtype=float32)
def sigmoid_activation(x):
""" Sigmoid activation function
Arguments
---------
x: tf.Tensor. Must be one of the following types: bfloat16, half, float32, float64, complex64, complex128.
"""
return 1/(1+tf.exp(-x))
## Solution
y = sigmoid_activation(tf.reduce_sum(tf.multiply(features, weights)) + bias)
print('label:\n', y)
label:
tf.Tensor([[0.3628656]], shape=(1, 1), dtype=float32)
¶ Multi-Layer Neural Network
That's how you can calculate the output for a single neuron. The real power of this algorithm happens when you start stacking these individual units into layers and stacks of layers, into a network of neurons. The output of one layer of neurons becomes the input for the next layer. With multiple input units and output units, we now need to express the weights as a matrix.

In the diagram above, the first layer shown on the bottom are the inputs, understandably called the input layer. The middle layer is called the hidden layer, and the final layer (on the top) is the output layer. We can express this network mathematically with matrices and use matrix multiplication to get linear combinations for each unit in one operation. For example, the hidden layer (comprised of units and ) can be calculated as follows:
The output for this small network is found by treating the hidden layer as inputs for the output unit. The network output is expressed simply as:
# Set the random seed so things are reproducible
tf.random.set_seed(7)
# Create 3 random input features
features = tf.random.normal((1,3))
# Define the size of each layer in our network
n_input = features.shape[1] # Number of input units, must match number of input features
n_hidden = 2 # Number of hidden units
n_output = 1 # Number of output units
# Create random weights connecting the inputs to the hidden layer
W1 = tf.random.normal((n_input,n_hidden))
# Create random weights connecting the hidden layer to the output layer
W2 = tf.random.normal((n_hidden, n_output))
# Create random bias terms for the hidden and output layers
B1 = tf.random.normal((1,n_hidden))
B2 = tf.random.normal((1, n_output))
## Solution
h = sigmoid_activation(tf.matmul(features, W1) + B1)
output = sigmoid_activation(tf.matmul(h, W2) + B2)
print(output)
tf.Tensor([[0.10678572]], shape=(1, 1), dtype=float32)
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
import tensorflow_datasets as tfds
tfds.disable_progress_bar()
Now we're going to build a larger network that can solve a (formerly) difficult problem, identifying text in an image. Here we'll use the MNIST dataset which consists of greyscale handwritten digits. Each image is 28x28 pixels, you can see a sample below

Our goal is to build a neural network that can take one of these images and predict the digit in the image.
First up, we need to get the dataset we are going to use to train and test our Neural Network. We will get our dataset using the tensorflow_datasets package. TensorFlow Datasets is a repository of datasets ready to use with TensorFlow. TensorFlow Datasets has a wide variety of datasets to train your machine learning models for many different tasks, ranging from text to video. For a full list of the datasets available in TensorFlow Datasets check out the TensorFlow Datasets Catalog.
The code below will load the MNIST dataset.
# Load training data
training_set, dataset_info = tfds.load('mnist', split = 'train', as_supervised = True, with_info = True)
[1mDownloading and preparing dataset 11.06 MiB (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to ~/tensorflow_datasets/mnist/3.0.1...[0m
[1mDataset mnist downloaded and prepared to ~/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.[0m
num_classes = dataset_info.features['label'].num_classes
print('There are {:,} classes in our dataset'.format(num_classes))
num_training_examples = dataset_info.splits['train'].num_examples
print('\nThere are {:,} images in the training set'.format(num_training_examples))
There are 10 classes in our dataset
There are 60,000 images in the training set
for image, label in training_set.take(1):
print('The images in the training set have:')
print('\u2022 dtype:', image.dtype)
print('\u2022 shape:', image.shape)
print('\nThe labels of the images have:')
print('\u2022 dtype:', label.dtype)
The images in the training set have:
• dtype: <dtype: 'uint8'>
• shape: (28, 28, 1)
The labels of the images have:
• dtype: <dtype: 'int64'>
for image, label in training_set.take(1):
image = image.numpy().squeeze()
label = label.numpy()
# Plot the image
plt.imshow(image, cmap = plt.cm.binary)
plt.colorbar()
plt.show()
print('The label of this image is:', label)
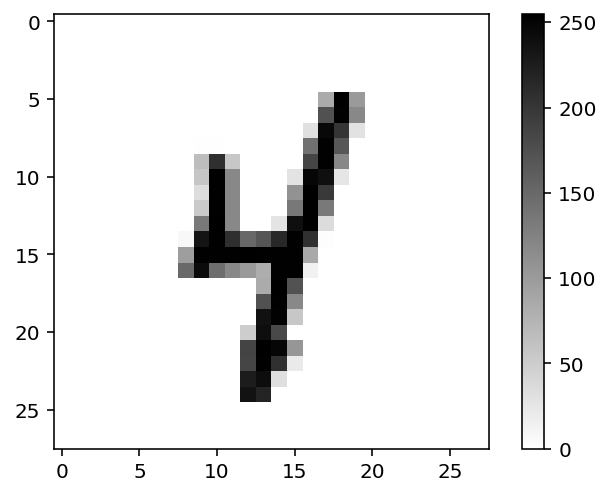
The label of this image is: 4
¶ Create Pipeline
As we can see, the pixel values of our images are in the range [0, 255]. We will now normalize the images and create a pipeline with our training set so that it can be fed into our neural network. In order to normalize the images we are going to divide the pixel values by 255. We will therefore, first change the dtype of our image from uint8 to float32 (32-bit single-precision floating-point numbers) using the tf.cast function.
def normalize(image, label):
image = tf.cast(image, tf.float32)
image /= 255
return image, label
batch_size = 64
training_batches = training_set.cache().shuffle(num_training_examples//4).batch(batch_size).map(normalize).prefetch(1)
¶ Build a Simple Neural Network
First, let's try to build a simple network for this dataset using weight matrices and matrix multiplications, just like we did in the previous notebook. Then, we'll see how to do it using TensorFlow and Keras, which provides a much more convenient and powerful method for defining network architectures.
The networks you've seen so far are called fully-connected or dense networks. Each unit in one layer is connected to each unit in the next layer. In fully-connected networks, the input to each layer must be a one-dimensional vector (which can be stacked into a 2D tensor as a batch of multiple examples). However, our images are 28 28 2D tensors, so we need to convert them into 1D vectors. Thinking about sizes, we need to convert the batch of images with shape (64, 28, 28, 1) to a have a shape of (64, 784), 784 is 28 times 28. This is typically called flattening, we flattened the 2D images into 1D vectors.
In the previous notebook, you built a network with one output unit. Here we need 10 output units, one for each digit. We want our network to predict the digit shown in an image, so what we'll do, is calculate the probabilities that the image is of any one digit or class. This ends up being a discrete probability distribution over the classes (digits) that tells us the most likely class for the image. That means we need 10 output units for the 10 classes (digits). We'll see how to convert the network output into a probability distribution next.
TODO: Flatten the batch of images
imagesthat we've created above. Then build a simple network with 784 input units, 256 hidden units, and 10 output units using random tensors for the weights and biases. For now, use a sigmoid activation function for the units in the hidden layer. Leave the output layer without an activation, we'll add one that gives us a probability distribution next. HINT: You can use thetf.reshape()function to flatten the batch of images.
images = list(training_batches.take(2))[0][0]
## Solution
def activation(x):
""" Sigmoid activation function
Arguments
---------
x: tf.Tensor. Must be one of the following types: bfloat16, half, float32, float64, complex64, complex128.
"""
return 1/(1+tf.exp(-x))
# Flatten the input images
inputs = tf.reshape(images, [images.shape[0], -1])
# Print the shape of the inputs. Should be (64,784)
print('The inputs have shape:', inputs.shape)
# Create Neural Network parameters
w1 = tf.random.normal((784,256))
b1 = tf.random.normal((1,256))
w2 = tf.random.normal((256,10))
b2 = tf.random.normal((1,10))
# Perform matrix multiplications for the hidden layer
# and apply activation function
h = activation(tf.matmul(inputs, w1) + b1)
# Perform matrix multiplication for the output layer
output = tf.matmul(h, w2) + b2
# Print the shape of the output. It should be (64,10)
print('The output has shape:', output.shape)
The inputs have shape: (64, 784)
The output has shape: (64, 10)
Now we have 10 outputs for our network. We want to pass in an image to our network and get out a probability distribution over the classes that tells us the most likely class(es) the image belongs to. Something that looks like this:

Here we see that the probability for each class is roughly the same. This is representing an untrained network, it hasn't seen any data yet so it just returns a uniform distribution with equal probabilities for each class.
To calculate this probability distribution, we often use the softmax function. Mathematically this looks like
What this does is squish each input between 0 and 1 and normalizes the values to give you a proper probability distribution where the probabilities sum up to one.
TODO: Implement a function
softmaxthat performs the softmax calculation and returns probability distributions for each example in the batch. Note that you'll need to pay attention to the shapes when doing this. If you have a tensorawith shape(64, 10)and a tensorbwith shape(64,), doinga/bwill give you an error because TensorFlow will try to do the division across the columns (called broadcasting) but you'll get a size mismatch. The way to think about this is the following: for each of the 64 examples, you only want to divide by one value, the sum in the denominator. So you needbto have a shape of(64, 1). This way TensorFlow will divide the 10 values in each row ofaby the one value in each row ofb. Pay attention to how you take the sum as well. You'll need to define theaxiskeyword intf.reduce_sum(). Settingaxis=0takes the sum across the rows whileaxis=1takes the sum across the columns. You will also need to use thekeepdimskeyword intf.reduce_sum()to make sure the output tensor has the correct shape(64,1).
## Solution
def softmax(x):
""" Softmax function
Arguments
---------
x: tf.Tensor. Must be one of the following types: bfloat16, half, float32, float64, complex64, complex128.
"""
return tf.exp(x) / tf.reduce_sum(tf.exp(x), axis = 1, keepdims = True)
# Apply softmax to the output
probabilities = softmax(output)
# Print the shape of the probabilities. Should be (64, 10).
print('The probabilities have shape:', probabilities.shape, '\n')
# The sum of probabilities for each of the 64 images should be 1
sum_all_prob = tf.reduce_sum(probabilities, axis = 1).numpy()
# Print the sum of the probabilities for each image.
for i, prob_sum in enumerate(sum_all_prob):
print('Sum of probabilities for Image {}: {:.1f}'.format(i+1, prob_sum))
The probabilities have shape: (64, 10)
Sum of probabilities for Image 1: 1.0
Sum of probabilities for Image 2: 1.0
Sum of probabilities for Image 3: 1.0
Sum of probabilities for Image 4: 1.0
Sum of probabilities for Image 5: 1.0
Sum of probabilities for Image 6: 1.0
Sum of probabilities for Image 7: 1.0
Sum of probabilities for Image 8: 1.0
Sum of probabilities for Image 9: 1.0
Sum of probabilities for Image 10: 1.0
Sum of probabilities for Image 11: 1.0
Sum of probabilities for Image 12: 1.0
Sum of probabilities for Image 13: 1.0
Sum of probabilities for Image 14: 1.0
Sum of probabilities for Image 15: 1.0
Sum of probabilities for Image 16: 1.0
Sum of probabilities for Image 17: 1.0
Sum of probabilities for Image 18: 1.0
Sum of probabilities for Image 19: 1.0
Sum of probabilities for Image 20: 1.0
Sum of probabilities for Image 21: 1.0
Sum of probabilities for Image 22: 1.0
Sum of probabilities for Image 23: 1.0
Sum of probabilities for Image 24: 1.0
Sum of probabilities for Image 25: 1.0
Sum of probabilities for Image 26: 1.0
Sum of probabilities for Image 27: 1.0
Sum of probabilities for Image 28: 1.0
Sum of probabilities for Image 29: 1.0
Sum of probabilities for Image 30: 1.0
Sum of probabilities for Image 31: 1.0
Sum of probabilities for Image 32: 1.0
Sum of probabilities for Image 33: 1.0
Sum of probabilities for Image 34: 1.0
Sum of probabilities for Image 35: 1.0
Sum of probabilities for Image 36: 1.0
Sum of probabilities for Image 37: 1.0
Sum of probabilities for Image 38: 1.0
Sum of probabilities for Image 39: 1.0
Sum of probabilities for Image 40: 1.0
Sum of probabilities for Image 41: 1.0
Sum of probabilities for Image 42: 1.0
Sum of probabilities for Image 43: 1.0
Sum of probabilities for Image 44: 1.0
Sum of probabilities for Image 45: 1.0
Sum of probabilities for Image 46: 1.0
Sum of probabilities for Image 47: 1.0
Sum of probabilities for Image 48: 1.0
Sum of probabilities for Image 49: 1.0
Sum of probabilities for Image 50: 1.0
Sum of probabilities for Image 51: 1.0
Sum of probabilities for Image 52: 1.0
Sum of probabilities for Image 53: 1.0
Sum of probabilities for Image 54: 1.0
Sum of probabilities for Image 55: 1.0
Sum of probabilities for Image 56: 1.0
Sum of probabilities for Image 57: 1.0
Sum of probabilities for Image 58: 1.0
Sum of probabilities for Image 59: 1.0
Sum of probabilities for Image 60: 1.0
Sum of probabilities for Image 61: 1.0
Sum of probabilities for Image 62: 1.0
Sum of probabilities for Image 63: 1.0
Sum of probabilities for Image 64: 1.0
¶ Building Neural Networks with TensorFlow and Keras
Keras is a high-level API to build and train neural networks. tf.keras is TensorFlow's implementation of the Keras API. In Keras, deep learning models are constructed by connecting configurable building blocks called layers. The most common type of model is a stack of layers called a Sequential model. The model is called sequential because it allows a tensor to be passed sequentially through the operations in each layer. In TensorFlow, the sequential model is implemented with tf.keras.Sequential.
In the cell below, we will use a Keras sequential model to build the same fully-connected neural network that we built in the previous section. Our sequential model will have three layers:
-
Input Layer:
tf.keras.layers.Flatten— This layer flattens the images by transforming a 2d-array of 28 28 pixels, to a 1d-array of 784 pixels (28 28 = 784). The first layer in a Sequential model needs to know the shape of the input tensors to the model. Since, this is our first layer, we need to specify the shape of our input tensors using theinput_shapeargument. Theinput_shapeis specified using a tuple that contains the size of our images and the number of color channels. It is important to note that we don't have to include the batch size in the tuple. The tuple can have integers orNoneentries, whereNoneentries indicate that any positive integer may be expected. -
Hidden Layer:
tf.keras.layers.Dense— A fully-connected (also known as densely connected) layer. For this layer we need to specify the number of neurons (or nodes) we want to use and the activation function. Note that we don't have to specify the shape of the input tensor to this layer, since Keras performs automatic shape inference for all layers except for the first layer. In this particular case, we are going to use256neurons with asigmoidactivation fucntion. -
Output Layer:
tf.keras.layers.Dense— A fully-connected layer with 10 neurons and a softmax activation function. The output values will represent the probability that the image is a particular digit. The sum of all the 10 nodes values is 1.
model = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape = (28,28,1)),
tf.keras.layers.Dense(256, activation = 'sigmoid'),
tf.keras.layers.Dense(10, activation = 'softmax')
])
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten (Flatten) (None, 784) 0
dense (Dense) (None, 256) 200960
dense_1 (Dense) (None, 10) 2570
=================================================================
Total params: 203,530
Trainable params: 203,530
Non-trainable params: 0
_________________________________________________________________
¶ Your Turn to Build a Neural Network

TODO: Create a network with 784 input units, a hidden layer with 128 units and a ReLU activation, then a hidden layer with 64 units and a ReLU activation, and finally an output layer with 10 units and a softmax activation function. You can use a ReLU activation function by setting
activation = 'relu'.
¶ Activation Functions
So far we've only been looking at the softmax activation, but in general any function can be used as an activation function. The only requirement is that for a network to approximate a non-linear function, the activation functions must be non-linear. Here are a few more examples of common activation functions: Tanh (hyperbolic tangent), and ReLU (rectified linear unit).

In practice, the ReLU function is used almost exclusively as the activation function for hidden layers.
¶ Looking at the Weights and Biases
Keras automatically initializes the weights and biases. The weights and biases are tensors attached to each of the layers you defined in your model. We can get all the weights and biases from our model by using the get_weights method. The get_weights method returns a list of all the weight and bias tensors in our model as NumPy arrays.
model_weights_biases = model.get_weights()
print(type(model_weights_biases))
<class 'list'>
print('\nThere are {:,} NumPy ndarrays in our list\n'.format(len(model_weights_biases)))
print(model_weights_biases)
There are 4 NumPy ndarrays in our list
[array([[-3.9461881e-02, 1.0994561e-02, 4.2317212e-03, ...,
-9.1556460e-04, -4.9699098e-02, -2.8802034e-02],
[ 5.7307526e-02, -3.6769409e-02, -6.1639901e-02, ...,
-9.7866803e-03, 5.2832738e-02, 4.4837072e-02],
[ 4.2089909e-02, 1.6957827e-02, -2.0909071e-02, ...,
3.9668456e-02, -1.8583562e-02, 4.5086943e-02],
...,
[ 1.9076601e-02, -9.1021135e-03, 5.0190434e-02, ...,
-3.3375092e-02, 1.5852839e-02, 5.6820244e-02],
[ 2.0846725e-05, 6.2416852e-02, -1.2588784e-02, ...,
6.1525375e-02, -6.0794689e-02, -1.4055882e-02],
[ 5.8459073e-02, 5.7663813e-02, 4.7769092e-02, ...,
-7.2663546e-02, -1.5190318e-03, 6.4568892e-02]], dtype=float32), array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0.], dtype=float32), array([[ 0.00259878, -0.00099388, -0.07238827, ..., -0.08519753,
0.01438402, 0.13676953],
[-0.11170821, 0.07627203, 0.14847681, ..., -0.1446782 ,
-0.03271004, -0.11684792],
[-0.04732816, 0.14730626, 0.1010685 , ..., -0.12424326,
-0.11944178, 0.08845438],
...,
[ 0.07201584, 0.0697287 , -0.04874112, ..., -0.1255357 ,
-0.1174299 , -0.14055479],
[ 0.14290121, 0.09786089, -0.05961406, ..., 0.14281815,
-0.09641024, -0.01075542],
[ 0.14462367, -0.01727054, -0.07247632, ..., -0.00777891,
0.12639049, 0.01719297]], dtype=float32), array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], dtype=float32)]
# Dislay the layers in our model
model.layers
[<keras.layers.core.flatten.Flatten at 0x7fcdbdf53f10>,
<keras.layers.core.dense.Dense at 0x7fcdcc3558d0>,
<keras.layers.core.dense.Dense at 0x7fcdcc320510>]
for i, layer in enumerate(model.layers):
if len(layer.get_weights()) > 0:
w = layer.get_weights()[0]
b = layer.get_weights()[1]
print('\nLayer {}: {}\n'.format(i, layer.name))
print('\u2022 Weights:\n', w)
print('\n\u2022 Biases:\n', b)
print('\nThis layer has a total of {:,} weights and {:,} biases'.format(w.size, b.size))
print('\n------------------------')
else:
print('\nLayer {}: {}\n'.format(i, layer.name))
print('This layer has no weights or biases.')
print('\n------------------------')
Layer 0: flatten
This layer has no weights or biases.
------------------------
Layer 1: dense
• Weights:
[[-3.9461881e-02 1.0994561e-02 4.2317212e-03 ... -9.1556460e-04
-4.9699098e-02 -2.8802034e-02]
[ 5.7307526e-02 -3.6769409e-02 -6.1639901e-02 ... -9.7866803e-03
5.2832738e-02 4.4837072e-02]
[ 4.2089909e-02 1.6957827e-02 -2.0909071e-02 ... 3.9668456e-02
-1.8583562e-02 4.5086943e-02]
...
[ 1.9076601e-02 -9.1021135e-03 5.0190434e-02 ... -3.3375092e-02
1.5852839e-02 5.6820244e-02]
[ 2.0846725e-05 6.2416852e-02 -1.2588784e-02 ... 6.1525375e-02
-6.0794689e-02 -1.4055882e-02]
[ 5.8459073e-02 5.7663813e-02 4.7769092e-02 ... -7.2663546e-02
-1.5190318e-03 6.4568892e-02]]
• Biases:
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
This layer has a total of 200,704 weights and 256 biases
------------------------
Layer 2: dense_1
• Weights:
[[ 0.00259878 -0.00099388 -0.07238827 ... -0.08519753 0.01438402
0.13676953]
[-0.11170821 0.07627203 0.14847681 ... -0.1446782 -0.03271004
-0.11684792]
[-0.04732816 0.14730626 0.1010685 ... -0.12424326 -0.11944178
0.08845438]
...
[ 0.07201584 0.0697287 -0.04874112 ... -0.1255357 -0.1174299
-0.14055479]
[ 0.14290121 0.09786089 -0.05961406 ... 0.14281815 -0.09641024
-0.01075542]
[ 0.14462367 -0.01727054 -0.07247632 ... -0.00777891 0.12639049
0.01719297]]
• Biases:
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
This layer has a total of 2,560 weights and 10 biases
------------------------
¶ Make Predictions
To make predictions on a batch of images with our model we use the .predict(image_batch) method. This method takes the images in our batch, feeds them to our network, performs a forward pass, and outputs a NumPy ndarray of shape (batch_size, num_classes) with the predicted probabilities for each image in the batch.
Since we have 64 images per batch (i.e. batch_size = 64) and our dataset has 10 classes (i.e. num_classes = 10), then our model will output an array of shape (64,10). The rows in this array hold the predicted probabilities for our images. Consequently, the first row holds the predicted probabilities for the first image in our batch; the second row holds the predicted probabilities for the second image in our batch; the third row holds the predicted probabilities for the third image in our batch; and so on. In this case, the predicted probabilities consist of 10 values, that is, one probability per class. Therefore, for each of the 64 images in our batch we will have 10 probabilities.
Let's plot our model's predicted probabilities for the first image in our batch.
for image_batch, label_batch in training_batches.take(1):
ps = model.predict(image_batch)
first_image = image_batch.numpy().squeeze()[0]
fig, (ax1, ax2) = plt.subplots(figsize=(6,9), ncols=2)
ax1.imshow(first_image, cmap = plt.cm.binary)
ax1.axis('off')
ax2.barh(np.arange(10), ps[0])
ax2.set_aspect(0.1)
ax2.set_yticks(np.arange(10))
ax2.set_yticklabels(np.arange(10))
ax2.set_title('Class Probability')
ax2.set_xlim(0, 1.1)
plt.tight_layout()
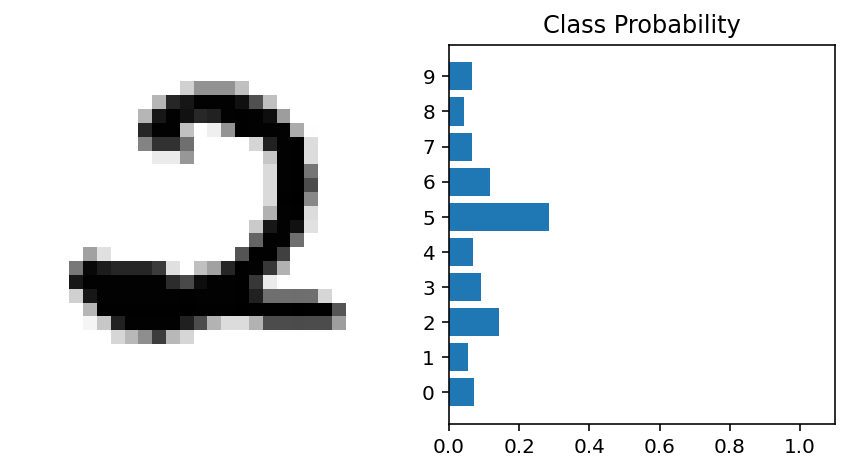
¶ Subclassing with TensorFlow and Keras
The tf.keras.Sequential model is a simple stack of layers that cannot be used to create arbitrary models. Luckily, tf.keras gives us the flexibility to build fully-customizable models by subclassing the tf.keras.Model and defining our own forward pass.
In the following example we will use a subclassed tf.keras.Model to build the same neural network as we built above with 784 inputs, 256 hidden units, and 10 output units. As before, we will use a ReLu activation function for the units in the hidden layer, and a Softmax activation function for the output neurons.
class Network(tf.keras.Model):
def __init__(self, num_classes = 2):
super().__init__()
self.num_classes = num_classes
# Define layers
self.input_layer = tf.keras.layers.Flatten()
self.hidden_layer = tf.keras.layers.Dense(256, activation = 'relu')
self.output_layer = tf.keras.layers.Dense(self.num_classes, activation = 'softmax')
# Define forward Pass
def call(self, input_tensor):
x = self.input_layer(input_tensor)
x = self.hidden_layer(x)
x = self.output_layer(x)
return x
¶ Let's go through this bit by bit.
class Network(tf.keras.Model):
Here we're inheriting from tf.keras.Model. Combined with super().__init__() this creates a class that provides a lot of useful methods and attributes. It is mandatory to inherit from tf.keras.Model when you're creating a class for your network. However, the name of the class itself can be anything.
We then create the layers of our network in the __init__ method and set them as attributes of the class instance. We also assign the number of neurons in our output layer in the __init__ method via the num_classes argument, which by default will have a value of 2.
self.input = tf.keras.layers.Flatten()
The first layer flattens the input image as we have discussed previously. We have given this layer the name self.input. We will use this name to reference this layer later. It doesn't matter what name you give your layers, you can name them whatever you want.
self.hidden = tf.keras.layers.Dense(256, activation = 'relu')
The second layer is a fully-connected (dense) layer with 256 neurons and a ReLu activation function. We have given this layer the name self.hidden. We will use this name to reference this layer later.
self.output = tf.keras.layers.Dense(self.num_classes, activation = 'softmax')
The third and last layer (output layer) is also a fully-connected (dense) layer with self.num_classes neurons and a softmax activation function. By default the number of output units will be 2, but can be defined to be any other integer depending on the number of output classes of your dataset.
Next, we define the forward pass in the call method.
def call(self, input_tensor):
TensorFlow models created with tf.keras.Model must have a call method defined. In the call method we take input_tensor and pass it through the layers we defined in the __init__ method.
x = self.input(input_tensor)
x = self.hidden(x)
x = self.output(x)
Here the input_tensor is passed through each layer and reassigned to x. We can see that the input_tensor goes through the input layer, then the hidden layer, and finally through the output layer. The order in which you define the layers in the __init__ method doesn't matter, but you'll need to sequence the layers correctly in the call method. Notice that we are referring to each layer in the __init__ method by the name we gave them. Remember this names are arbitrary.
Now that we have defined our model class we can create a model object. Note that we didn't specify the shape of our input tensor in our Network class. In this case, the weights and biases will only be initialized when we build our model by calling build(batch_input_shape) or when the first call to a training/evaluation method (such as .fit or .evaluate) is made. We call this a delayed-build pattern.
So, now let's create a model object and build it (i.e. initialize its weights and biases) by calling build().
# Create a model object
subclassed_model = Network(10)
# Build the model, i.e. initialize the model's weights and biases
subclassed_model.build((None, 28, 28, 1))
subclassed_model.summary()
¶ Training Neural Networks
The network we built in the previous part isn't so smart, it doesn't know anything about our handwritten digits. Neural networks with non-linear activations work like universal function approximators. There is some function that maps your input to the output. For example, images of handwritten digits to class probabilities. The power of neural networks is that we can train them to approximate this function, and basically any function given enough data and compute time.

At first the network is naive, it doesn't know the function mapping the inputs to the outputs. We train the network by showing it examples of real data, then adjusting the network parameters such that it approximates this function.
To find these parameters, we need to know how poorly the network is predicting the real outputs. For this we calculate a loss function (also called the cost), a measure of our prediction error. For example, the mean squared loss is often used in regression and binary classification problems
where is the number of training examples, are the true labels, and are the predicted labels.
By minimizing this loss with respect to the network parameters, we can find configurations where the loss is at a minimum and the network is able to predict the correct labels with high accuracy. We find this minimum using a process called gradient descent. The gradient is the slope of the loss function and points in the direction of fastest change. To get to the minimum in the least amount of time, we then want to follow the gradient (downwards). You can think of this like descending a mountain by following the steepest slope to the base.

¶ Load the Dataset
training_set, dataset_info = tfds.load('mnist', split='train', as_supervised = True, with_info = True)
def normalize(image, label):
image = tf.cast(image, tf.float32)
image /= 255
return image, label
num_training_examples = dataset_info.splits['train'].num_examples
batch_size = 64
training_batches = training_set.cache().shuffle(num_training_examples//4).batch(batch_size).map(normalize).prefetch(1)
model = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape = (28, 28, 1)),
tf.keras.layers.Dense(128, activation = 'relu'),
tf.keras.layers.Dense(64, activation = 'relu'),
tf.keras.layers.Dense(10, activation = 'softmax')
])
¶ Getting the Model Ready For Training
Before we can train our model we need to set the parameters we are going to use to train it. We can configure our model for training using the .compile method. The main parameters we need to specify in the .compile method are:
-
Optimizer: The algorithm that we'll use to update the weights of our model during training. Throughout these lessons we will use the
adamoptimizer. Adam is an optimization of the stochastic gradient descent algorithm. For a full list of the optimizers available intf.kerascheck out the optimizers documentation. -
Loss Function: The loss function we are going to use during training to measure the difference between the true labels of the images in your dataset and the predictions made by your model. In this lesson we will use the
sparse_categorical_crossentropyloss function. We use thesparse_categorical_crossentropyloss function when our dataset has labels that are integers, and thecategorical_crossentropyloss function when our dataset has one-hot encoded labels. For a full list of the loss functions available intf.kerascheck out the losses documentation. -
Metrics: A list of metrics to be evaluated by the model during training. Throughout these lessons we will measure the
accuracyof our model. Theaccuracycalculates how often our model's predictions match the true labels of the images in our dataset. For a full list of the metrics available intf.kerascheck out the metrics documentation.
These are the main parameters we are going to set throught these lesson. You can check out all the other configuration parameters in the TensorFlow documentation
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
¶ Taking a Look at the Loss and Accuracy Before Training
Before we train our model, let's take a look at how our model performs when it is just using random weights. Let's take a look at the loss and accuracy values when we pass a single batch of images to our un-trained model. To do this, we will use the .evaluate(data, true_labels) method. The .evaluate(data, true_labels) method compares the predicted output of our model on the given data with the given true_labels and returns the loss and accuracy values.
for image_batch, label_batch in training_batches.take(1):
loss, accuracy = model.evaluate(image_batch, label_batch)
print('\nLoss before training: {:,.3f}'.format(loss))
print('Accuracy before training: {:.3%}'.format(accuracy))
2/2 [==============================] - 0s 10ms/step - loss: 2.3351 - accuracy: 0.0312
Loss before training: 2.335
Accuracy before training: 3.125%
EPOCHS = 5
history = model.fit(training_batches, epochs = EPOCHS)
Epoch 1/5
938/938 [==============================] - 6s 5ms/step - loss: 0.2719 - accuracy: 0.9214
Epoch 2/5
938/938 [==============================] - 3s 3ms/step - loss: 0.1118 - accuracy: 0.9663
Epoch 3/5
938/938 [==============================] - 3s 3ms/step - loss: 0.0774 - accuracy: 0.9767
Epoch 4/5
938/938 [==============================] - 3s 3ms/step - loss: 0.0591 - accuracy: 0.9816
Epoch 5/5
938/938 [==============================] - 3s 3ms/step - loss: 0.0473 - accuracy: 0.9850
The .fit method returns a History object which contains a record of training accuracy and loss values at successive epochs, as well as validation accuracy and loss values when applicable. We will discuss the history object in a later lesson.
With our model trained, we can check out it's predictions.
for image_batch, label_batch in training_batches.take(1):
ps = model.predict(image_batch)
first_image = image_batch.numpy().squeeze()[0]
fig, (ax1, ax2) = plt.subplots(figsize=(6,9), ncols=2)
ax1.imshow(first_image, cmap = plt.cm.binary)
ax1.axis('off')
ax2.barh(np.arange(10), ps[0])
ax2.set_aspect(0.1)
ax2.set_yticks(np.arange(10))
ax2.set_yticklabels(np.arange(10))
ax2.set_title('Class Probability')
ax2.set_xlim(0, 1.1)
plt.tight_layout()

for image_batch, label_batch in training_batches.take(1):
loss, accuracy = model.evaluate(image_batch, label_batch)
print('\nLoss after training: {:,.3f}'.format(loss))
print('Accuracy after training: {:.3%}'.format(accuracy))
2/2 [==============================] - 0s 7ms/step - loss: 0.0314 - accuracy: 0.9844
Loss after training: 0.031
Accuracy after training: 98.438%